Come misurare la vulnerabilità dei conti pubblici
Questo articolo riporta una breve sintesi dei risultati di una ricerca che la Fondazione David Hume ha condotto negli ultimi anni sulla vulnerabilità dei conti pubblici delle economie avanzate[1].
1. A che serve una misura di vulnerabilità
Quando un paese ha un debito pubblico troppo elevato, gli investitori richiedono tassi di interesse più alti per sottoscrivere i suoi titoli di Stato: il rischio di non essere rimborsati, o di esserlo solo in parte, innalza il prezzo del prestito concesso. Accade così che i rendimenti dei titoli del debito pubblico possano toccare livelli molto alti, anche al di sopra dei tassi che normalmente vengono considerati usurari. Nel caso della Grecia, ad esempio, al culmine della crisi (febbraio 2012), i tassi sono arrivati a sfiorare il 30%. Quanto all’Italia, c’è stato un momento, alla fine del 2011, in cui i tassi si sono avvicinati pericolosamente alla soglia dell’8%, da molti considerata un punto critico, oltre il quale diventa pericolosissimo spingersi.
Ma come fa un paese a proteggersi contro i rischi di una crisi del suo debito sovrano? Come fa a sapere in anticipo che potrebbe sopravvenire una crisi? Come fa ad accorgersi che è seduto sopra una polveriera? Come fa, in altre parole, a misurare la propria vulnerabilità?
Apparentemente, la risposta è semplice: basta non indebitarsi troppo. Ma questa è una risposta insoddisfacente. Non solo perché non tutti i paesi sono come la Germania, che ha un’economia capace di crescere senza aumentare il debito, ma perché il nesso fra debito pubblico e rendimenti non è lineare: esistono paesi, come il Giappone, che riescono ad approvvigionarsi sui mercati a tassi molto bassi nonostante un enorme rapporto debito/Pil (oltre il 200%), ed esistono paesi, come la Romania, che sono costretti a pagare tassi relativamente elevati a dispetto di un rapporto debito/Pil molto contenuto.
Si potrebbe allora pensare di usare direttamente i rendimenti dei titoli di Stato, eventualmente corretti per l’inflazione, come misure di vulnerabilità. Questa strada, tuttavia, è resa impraticabile da almeno due circostanze.
La prima è che i mercati attraversano lunghi periodi di sonno, nei quali letteralmente ignorano le differenze fra paesi. È stato questo il caso dei primi 9-10 dieci anni dell’euro, nei quali i tassi richiesti a paesi come la Germania sono stati analoghi a quelli richiesti a paesi come la Grecia.
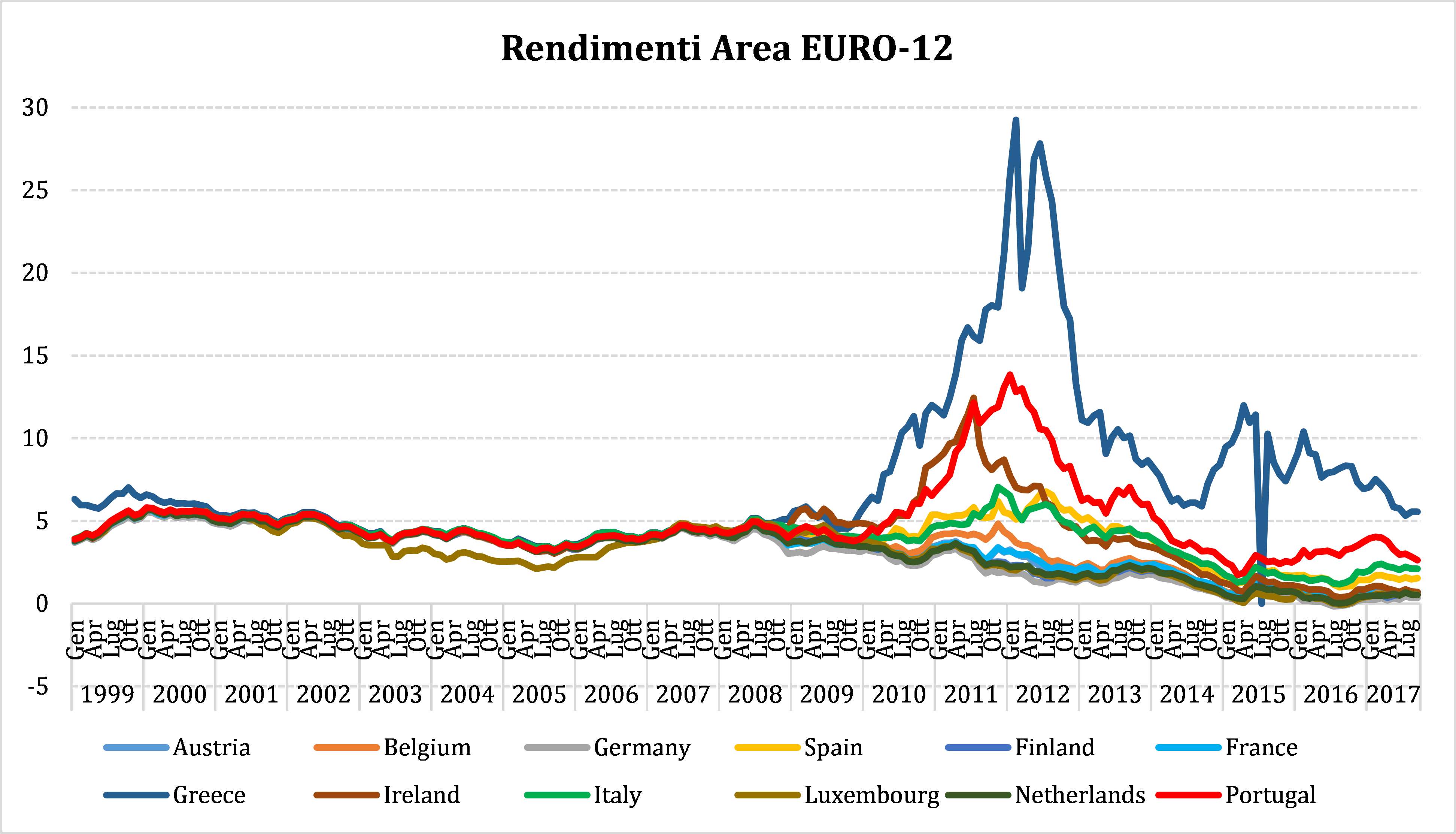(Fonte:ECB)
La seconda circostanza è che i tassi sono fortemente condizionati dalla politica monetaria delle banche centrali, che può sostenere artificialmente i corsi dei titoli di Stato di un paese o, nel caso della Banca centrale Europea durante la crisi, di un gruppo di paesi deboli o ritenuti tali.
Se né il rapporto debito/pil né i tassi di mercato sono un buon metro per valutare la vulnerabilità dei conti pubblici, si potrebbe puntare sulle valutazioni dei debiti sovrani forniti dalle maggiori agenzie di rating, le “tre sorelle” Moody’s, Fitch e Standard and Poors’, con le loro scale a una ventina di posti, da AAA a D. Sarebbe ragionevole, in altre parole, supporre che il rating sia una sorta di termometro della salute dei conti pubblici. Quando il rating è buono (tripla o doppia A) i conti pubblici del paese non corrono rischi, quando è cattivo (B) o pessimo (C) gli interessi sui titoli di Stato tendono ad essere elevati e rischiano di subire drastici incrementi in caso di crisi.
Sfortunatamente, tuttavia, anche questa strada non funziona bene, per diversi motivi. Il primo è che anche le Agenzie di rating, come i mercati, attraversano periodi di sonno, in cui non si accorgono delle enormi differenze di vulnerabilità che sussistono fra paesi.
Il secondo è che, tendenzialmente, il giudizio delle Agenzie segue e non precede quello dei mercati. Una misura di vulnerabilità dovrebbe essere predittiva e non postdittiva del comportamento dei mercati.
La realtà è che sia le Agenzie di rating sia i mercati sono due black box di cui non conosciamo i circuiti interni ma di cui sappiamo che funzionano in modi diversi, spesso molto diversi. Una comparazione sistematica delle valutazioni delle Agenzie e di quelle dei mercati su 24 paesi (quelli con informazioni complete) dal 1999 al 2016 ha rivelato che i casi di valutazioni coerenti sono più o meno quanti i casi di valutazioni incoerenti o in aperto conflitto (con le Agenzie che indicano un miglioramento quando i mercati segnalano un peggioramento; o viceversa).
Eppure, conoscere il grado di vulnerabilità dei conti pubblici di un paese sarebbe essenziale, per gli investitori come per i governanti. Se vulnerabilità significa, essenzialmente, esposizione al rischio di aumenti futuri dei tassi, una misura di vulnerabilità può essere una guida preziosa per implementare strategie di selezione del portafoglio che tengano conto di fattori (di debolezza o di forza) che sono già presenti, ma di cui i mercati potrebbero accorgersi solo in futuro, quando una crisi dovesse esplodere o viceversa rientrare.
Quanto ai governi, è chiaro che una misura di vulnerabilità dei conti pubblici capace di anticipare evoluzioni future li proteggerebbe da due rischi, uno ovvio, l’altro più sottile. Quello ovvio è di non risanare i conti pubblici solo perché i mercati non si sono ancora accorti della malattia, un’eventualità che ben si attaglia ai casi di Grecia, Portogallo, Italia, che nel primo decennio dell’euro hanno immeritatamente beneficiato del doppio sonno dei mercati e delle Agenzie. Il secondo rischio da cui una misura di vulnerabilità accurata potrebbe proteggere un paese e il suo governo, è quello di subire, nei periodi di crisi, una valutazione dei mercati e delle Agenzie peggiore di quella che la salute di suoi conti pubblici giustificherebbe.
Ecco perché può essere utile disporre di un indice che misuri il grado di vulnerabilità dei conti pubblici.
2. Indice VS e mente dei mercati
A questo scopo, come FDH, abbiamo messo a punto l’indice VS, o indice di Vulnerabilità Strutturale. L’idea-base su cui poggia l’indice VS è di misurare lo stato di salute dei conti pubblici di un paese in un modo che, al tempo stesso, rifletta la “mente dei mercati”, ossia il modo in cui i mercati giudicano i conti pubblici di un paese, e nello stesso tempo non sia sensibile agli elementi contingenti (fluttuazioni di breve periodo, politica monetaria espansiva o restrittiva) che in un particolare momento concorrono alla formazione dei rendimenti dei titoli di Stato.
L’unità di misura dell’indice sono i punti-base, e la sua interpretazione è la seguente: l’indice VS misura i rendimenti che, in base ai suoi fondamentali, dovrebbero avere i titoli di Stato di un paese se i mercati lo giudicassero con i parametri che mediamente hanno utilizzato negli anni 2009-2016, ossia nel periodo successivo al fallimento di Lehman Brothers.
L’indice è stato calcolato per 40 economie avanzate, o relativamente avanzate[2], per tutti gli anni che vanno dall’introduzione dell’euro (1° gennaio 1999) al 2016. Attualmente stiamo lavorando a una nuova versione dell’indice, con cadenza più frequente (trimestre o mese), e capacità di stimare anticipatamente il consuntivo dell’anno in corso.
Ed ecco, in estrema sintesi, alcuni risultati.
1. L’equazione dell’indice permette di scoprire quali sono, per la “mente dei mercati”, i fondamentali che contano e quelli che non contano, e soprattutto quanto contano, ossia quali effetti hanno sui rendimenti; sorprendentemente fra i parametri che non contano c’è il deficit pubblico, mentre un’importanza cruciale rivestono il debito pubblico detenuto da investitori esteri, l’inflazione e la competitività.
2. Applicato al periodo 1999-2016 l’indice VS mette in evidenza il deterioramento dei conti pubblici di Grecia, Portogallo, con molti anni di anticipo (dai primi anni 2000), quando né i mercati né le Agenzie di rating emettevano segnali di rischio.
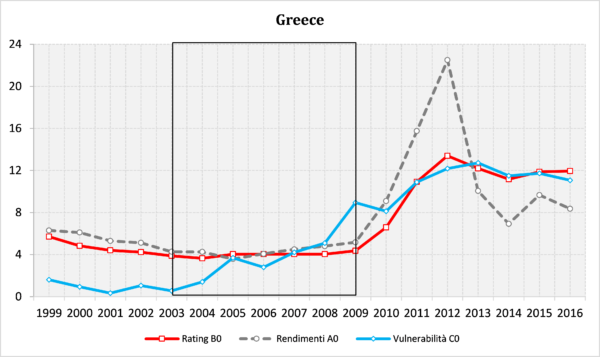
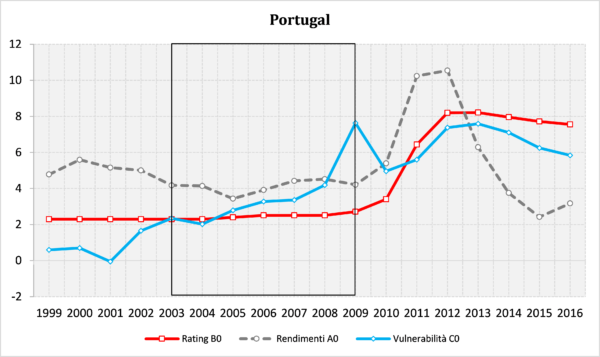
Come si vede l’indice di vulnerabilità strutturale (linea azzurra) punta decisamente verso l’alto a partire dal 2003-2004 sia in Grecia sia in Portogallo.
Quanto agli altri due paesi che hanno dovuto chiedere aiuto alla Troika (Spagna e Irlanda) l’indice VS mette in evidenza il deterioramento dei rispettivi conti pubblici con qualche anno di anticipo (dal 2006-2007 in Spagna, dal 2006-2008 in Irlanda).
4. Nel caso dell’Italia, la serie storica dell’indice VS mostra che:
a) la tendenza di lungo periodo (dal 2000 al 2009) della vulnerabilità strutturale è all’aumento;
b) tuttavia, nel periodo immediatamente precedente la crisi di fine 2011, la vulnerabilità era in sia pur lieve diminuzione;
c) negli ultimi 4 anni la vulnerabilità strutturale tende a diminuire in termini assoluti, ma ad aumentare in termini relativi, ossia rispetto alle altre economie avanzate.
3. Indice VS, rating delle Agenzie, rendimenti
Forse il modo più efficace di usare l’indice VS è di metterlo a confronto con gli altri due principali strumenti di valutazione della salute dei conti pubblici, ossia i rendimenti dei titoli di Stato decennali sui mercati e il rating dei debiti sovrani forniti dalle Agenzie. Il primo confronto (con i mercati) può essere effettuato direttamente, perché l’indice VS è espresso in punti base, ovvero può essere interpretato come una sorta di rendimento “dovuto”: l’indice VS indica quali rendimenti richiederebbero i mercati se si basassero esclusivamente sui fondamentali e si comportassero con il livello medio di severità espresso nel periodo 2009-2016, allorché – a differenza che nel decennio di esordio dell’euro – erano “all’erta” e non “in sonno”.
Per il secondo confronto, dato che le Agenzie di rating adottano scale ordinali, le abbiamo convertite in punti base, imponendo la medesima media e la medesima deviazione standard osservate per i rendimenti. Inoltre, per il 2017, per il quale si hanno solo dati parziali, abbiamo effettuato una stima del valore dell’indice VS utilizzando tutta l’informazione disponibile fino a ottobre.
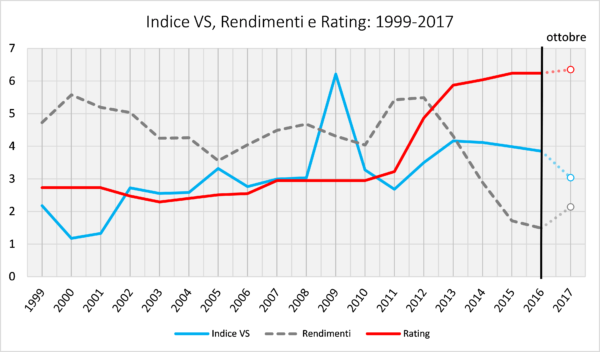
Il risultato è piuttosto chiaro, e si può riassumere in quattro punti.
Primo. Nonostante gli sforzi di risanamento dei governi Monti e Letta, fra il 2011 e il 2013 la vulnerabilità dei nostri conti pubblici (linea azzurra) è aumentata di circa 150 punti base. Questo cambiamento è stato iper-segnalato dalle agenzie di rating, ma non dai mercati, che hanno invece reagito con una riduzione dei rendimenti.
Secondo. Fra il 2013 e il 2016 l’indice VS di vulnerabilità strutturale è rimasto sostanzialmente stabile (lievissimo miglioramento[3]), mentre gli altri due indici, ovvero il rating delle agenzie (linea rossa) e i rendimenti sui mercati (linea grigia tratteggiata) si sono mossi in direzioni opposte: le Agenzie hanno ulteriormente penalizzato l’Italia, i mercati hanno concesso rendimenti sempre più bassi.
Terzo. Come conseguenza di questi andamenti, il 2016 ha registrato il massimo di divaricazione fra il giudizio delle Agenzie e quello dei mercati, con uno scarto che – adottando una scala comune – è arrivato a sfiorare i 500 punti base.
Quarto. Nel 2017, secondo le nostre stime, la vulnerabilità strutturale dell’Italia (indice VS) mostra un significativo miglioramento, proprio mentre il giudizio dei mercati (rendimenti) si fa più severo. Quel che ne risulta è una convergenza fra le due traiettorie, che ora paiono fornire sostanzialmente la medesima valutazione sulla salute dei nostri conti pubblici. Del tutto opposto è l’andamento del rating delle Agenzie, che risente del declassamento del debito italiano BBB+ a BBB operato da Fitch nel mese di aprile.
La conclusione è amara: troppo tenere, o troppo distratte, quando avrebbero dovuto avvertitici della debolezza dei nostri fondamentali, le Agenzie di rating appaiono invece troppo severe oggi che i nostri conti stanno migliorando. Non sarebbe un problema se, dal rating delle Agenzie, non dipendessero pesantemente le scelte dei grandi investitori internazionali. E, soprattutto, se da tempo non si parlasse di nuove regole per valutare i titoli di Stato detenuti dalle banche: ove il valore di questi dovesse essere alterato in funzione del rating delle Agenzie, la tendenza delle Agenzie stesse a sopravvalutare il grado di vulnerabilità dell’Italia potrebbe costarci piuttosto cara.
Da questo punto di vista disporre di un indice che dipende solo dai fondamentali, insensibile sia agli umori dei mercati sia alle valutazioni, presumibilmente anche (lato sensu) “politiche”, della Agenzie di rating, potrebbe rivelarsi uno stimolo a fare di più quando siamo sopravvalutati e uno scudo per difendere la nostra reputazione quando siamo gravemente penalizzati.
[1] La ricerca ha usufruito di un contributo della Compagnia di San Paolo.
[2] Per economie avanzate o relativamente avanzate (o paesi ERA) intendiamo tutti i paesi europei, o extraeuropei ma appartenenti all’Ocse (41 paesi in tutto). Nella nostra analisi ne abbiamo considerati 40 perché nel caso dell’Estonia mancano i dati dei rendimenti dei titoli di Stato.
[3] Al lieve miglioramento in termini assoluti si è accompagnato invece un netto peggioramento relativamente agli altri paesi.
