Controlled Mechanical Ventilation (CMV) works

1. Research

The Marche Region financed, in March 2021, a tender for the purchase and installation of Controlled Mechanical Ventilation (CMV) systems in school classrooms. The aim was to ensure face-to-face lessons, as the available scientific evidence indicated that Controlled Mechanical Ventilation (CMV) was an effective tool to counter the spread of Sars-CoV-2, reducing the permanence of pollutants in the air. The applications were  187, for a total of 3,027 classrooms distributed in 323 schools in the Marche region, for a funded amount of 9 million euros. The first schools benefiting from the funding, set up mechanical ventilation systems during the summer period, in order to start school with active and properly functioning equipment. On this basis, with the collaboration of Hume Foundation, in 2021/2022 a study was developed allowing the comparison between two sets of observations:

1) In the first group: classes with the installation of Controlled Mechanical Ventilation (more than 300, 3% of the classes total)

2) In the second set: classes without mechanical ventilation.

This comparison was structured by analyzing the incidence data (the new positive cases) from Sars-CoV-2 in the two sets under observation (classes with CMV vs classes without ventilation) involving all school levels, from kindergarten to upper secondary school.

On this premise, the Hume Foundation asked the Marche Region to analyze the data collected, in order to estimate the effectiveness of CMV in counteracting the infection’s transmission.

For this purpose, a number of mathematical-statistical models have been built, designed to assess the impact of CMV on the transmission risk, net of other effects such as the order of the school and the number of pupils per class.

2. Methods

To estimate the effectiveness of the CMV, two transmission indicators in particular were used, both based on the cases clusters count (2 or more cases within the same class). The impact of CMV was evaluated both in a rough way, i.e. by comparing the values ​​of the two indicators on homogeneous class groups in terms of air changes per hour, and with regression techniques, keeping under control the number of pupils per class and the type of school.

Among the many estimates of the CMV effectiveness obtained, the most conservative were usually selected.

3. Main result

The risk of transmission can be estimated by calculating, for each class, the ratio between the number of cases related to infections occurring within the class and the number of exposed, ie pupils per class.

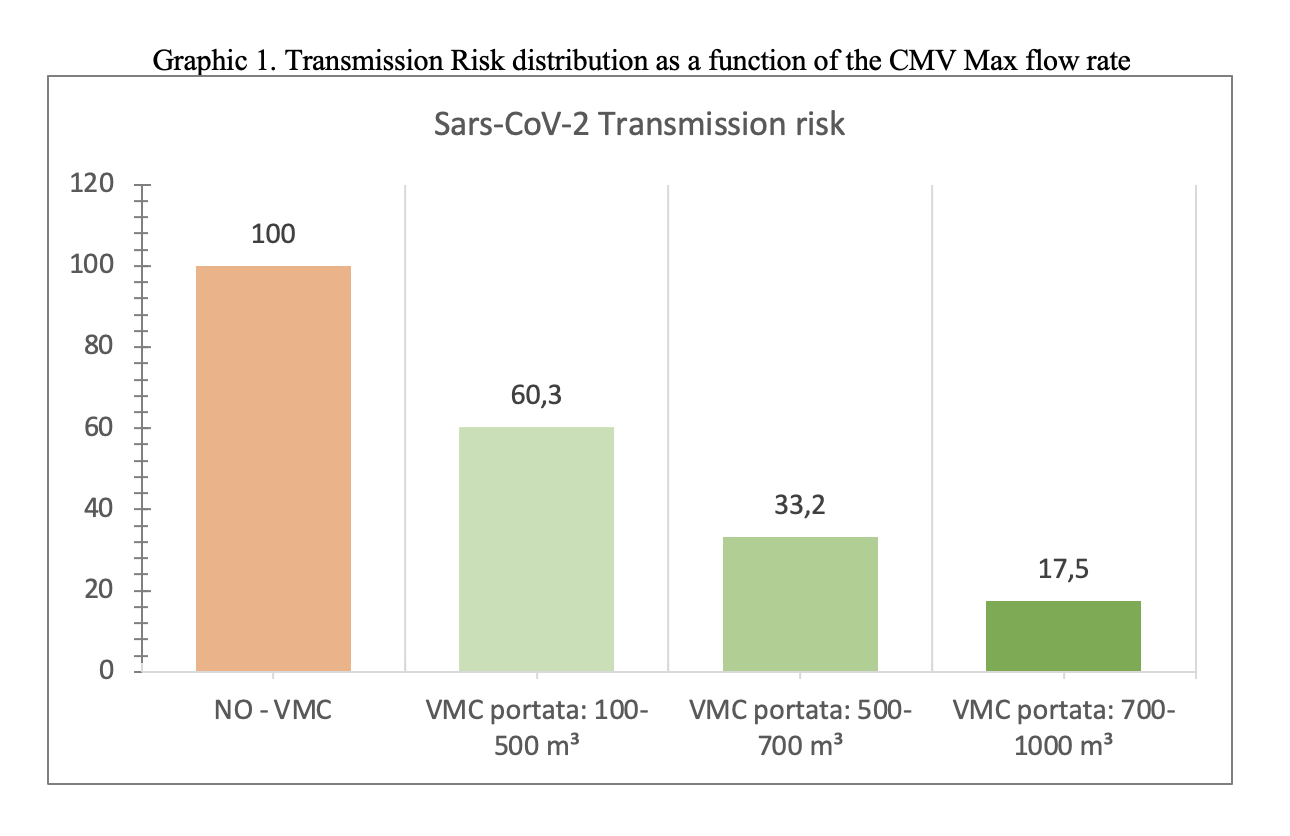
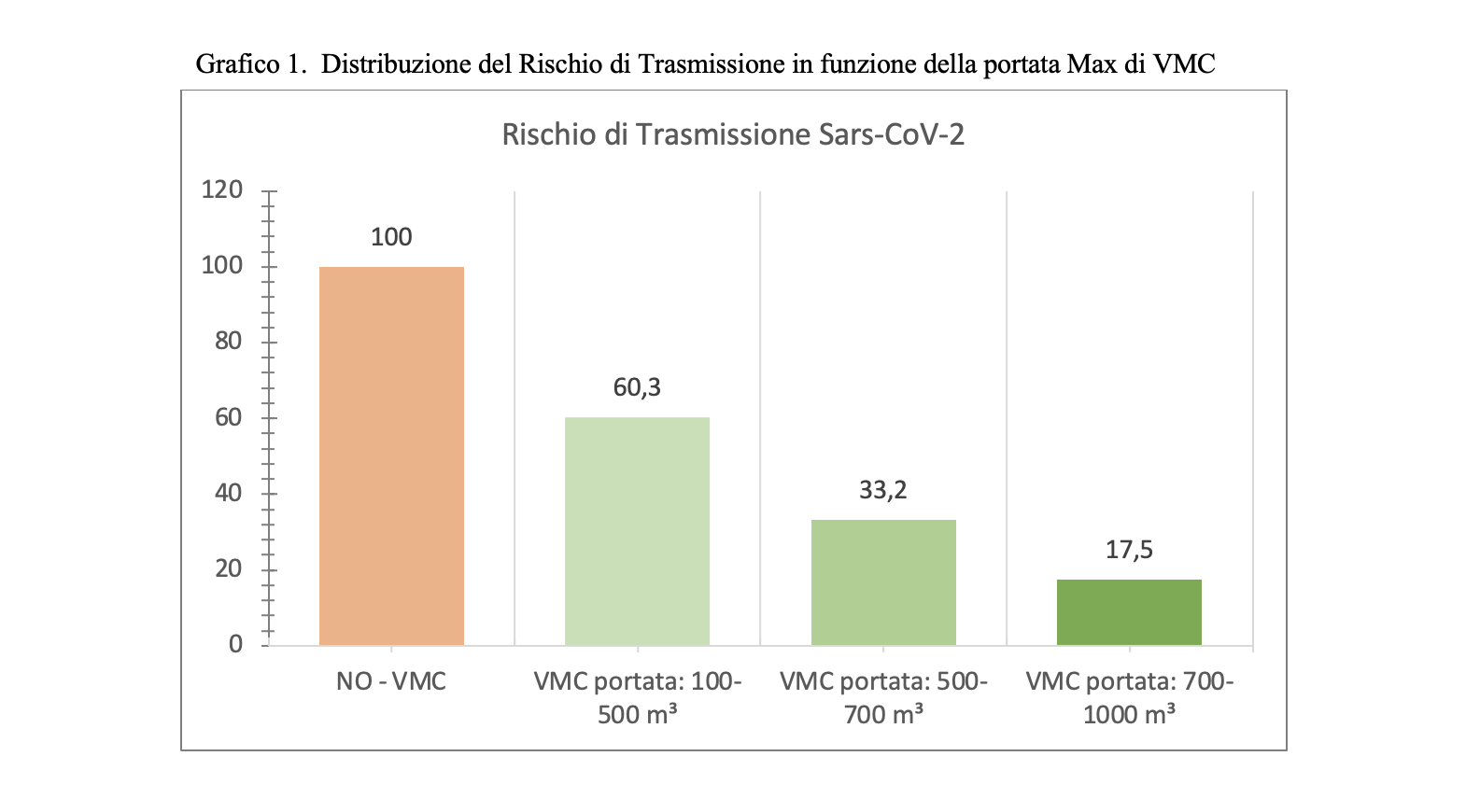
By setting the indicator value for classes without CMV to 100, you can determine the relative risk of infection for classrooms equipped with CMV. This ratio is equal to 37.2%, which means that the presence of CMV reduces the risk of transmission by a factor close to 3 (average indicator).

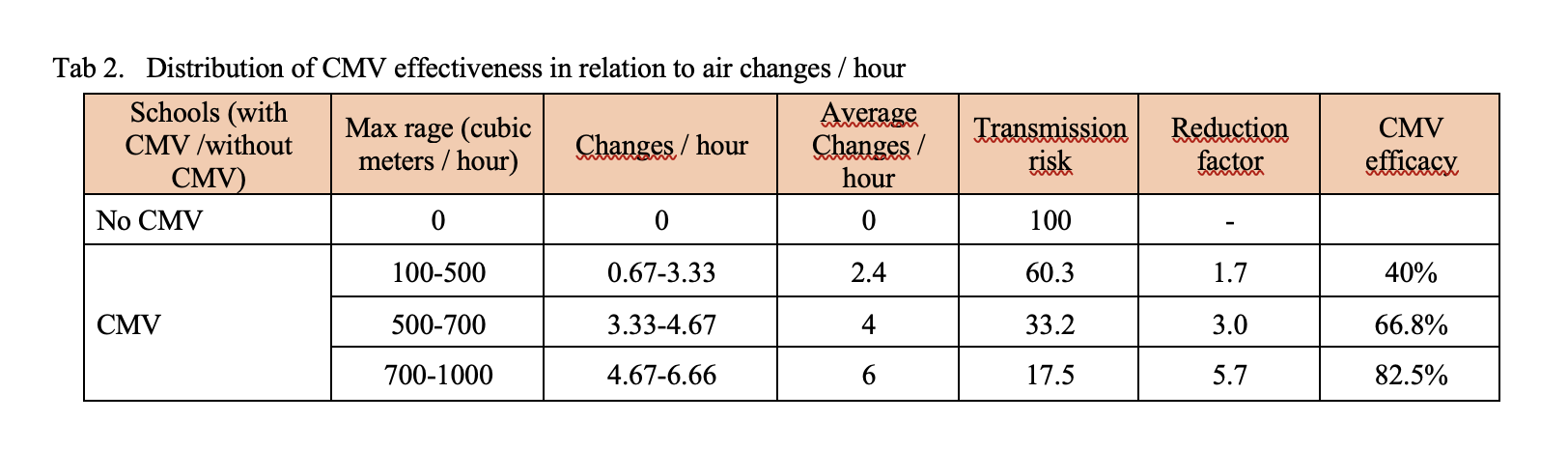
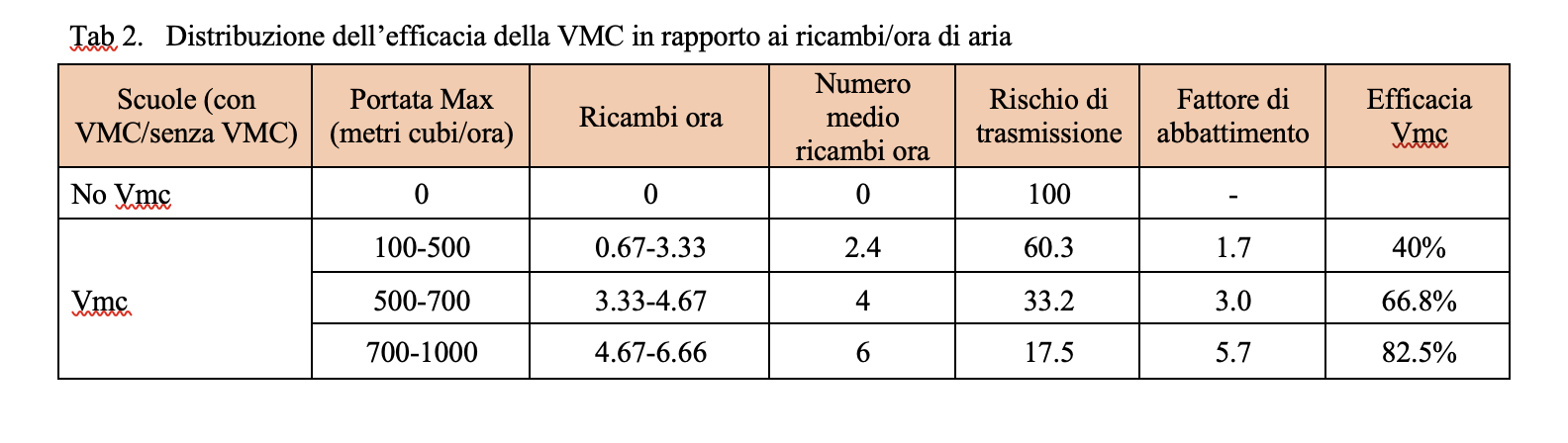
The maximum capacity of the devices installed varies considerably from school to school, in a range that goes from 100 to 1000 cubic meters-hour. If we distinguish the classes on the capacity of the installed systems, we discover that the relative risk can drop to a value more or less between 5 and 6 if the flow rate exceeds 750 cubic meters per hour, which is equivalent – approximately – to 5 changes per hour. .

All this can be summarized by calculating how the risk reduction factor increases as the quality of CMV increases, measured by the number of air changes.

As indicated in table 1, the transmission indicator varies based on the presence of schools with CMV / without CMV or with a different flow rate of cubic meters / hour. A change in efficacy is observed from: 40% correlated to a turnover / hour of 0.67-3.33, to a 66.8% efficacy correlated with 3.33 – 4.67 replacement / hour at 82.5 % efficacy with 4.67-6.66 replacement / hour.

It’s clear that the CMV, especially if adequately sized (6 or more air changes-hour), has the ability to reduce the Sars-CoV-2 infection risk by over 80%. Using it in schools, we could switch from an incidence rate of 250 per 100,000 (risk threshold identified by the Ministry) to a rate of 50 per 100,000.

Surprisingly, the risk reduction factor (between 5 and 6), inferred from this field research, corresponds perfectly to that obtained from the studies of engineers and air quality experts, based on controlled experiments (see Mikszewski, A., Stabile, L., Buonanno, G., Morawska, L., Increased close proximity airborne transmission of the SARS-CoV-2 Delta variant, “Science of the Total Environment”, 816, 2022).

4. Data information

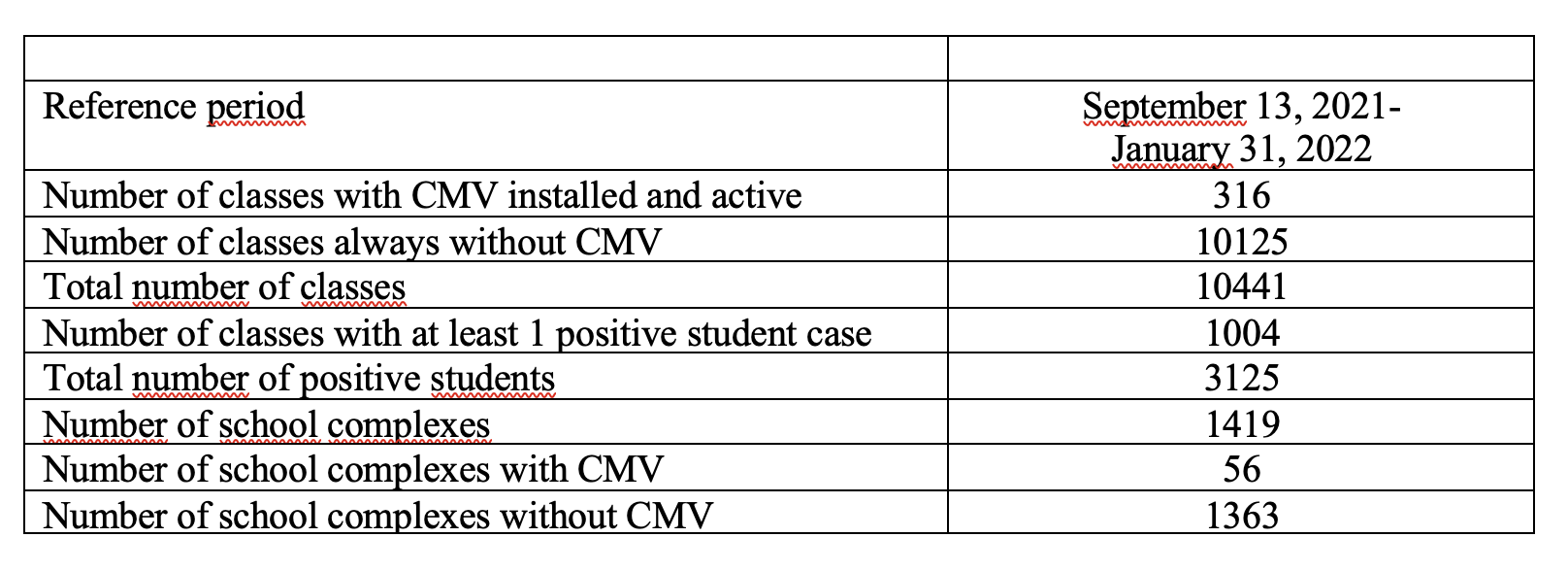
The final data set is a file with 10465 records (equal to the number of classes), each described by 21 variables (plus the class and school identification fields).

The fundamental variables that describe each class are the following:

– province

– plexus

– school order

– section

– year

– number of pupils in the class

– number of positive students in 12 different periods

– presence / absence of the CMV

– CMV plant brand

– CMV system model

The 12 periods correspond to the weeks, except for the initial one, which runs from 13 September to 10 October, and the final one, which runs from 7 to 31 January.

The classes considered are all those without CMV (10125), plus all those with CMV since 13 September (316 out of 340): in all 10441 classes.

Finally, here is some brief information on the classes considered.

For this first phase of the study, the percentage of classes taken into consideration is equal to 3% of the total.

Conferenza stampa 22 marzo 2022

La ventilazione meccanica controllata (Vmc) funziona

1. La ricerca

La Regione Marche ha finanziato, nel marzo 2021, un bando per l’acquisto e l’installazione degli impianti di Ventilazione Meccanica Controllata (VMC) nelle aule scolastiche. L’intervento era finalizzato a garantire le lezioni in presenza, in quanto le evidenze scientifiche disponibili indicavano nella Ventilazione Meccanica Controllata (VMC) un efficace strumento per contrastare la diffusione di Sars-CoV-2, riducendo la permanenza degli elementi inquinanti nell’aria. Le domande risultavano essere complessivamente n.187, per un totale 3.027 aule distribuite in 323 scuole marchigiane, per un importo finanziato di 9 milioni di euro. Le prime scuole beneficiarie del finanziamento, nel periodo estivo predisponevano gli impianti di ventilazione meccanica, al fine di iniziare l’anno scolastico con la strumentazione attiva e correttamente funzionante. Su queste basi nel 2021/2022 con la collaborazione della fondazione Hume, si è sviluppato uno studio che permetteva la comparazione tra due insiemi di osservazioni:

• Nel primo insieme: le classi con l’istallazione della Ventilazione Meccanica Controllata VMC (più di 300, il 3% sul totale delle classi)
• Nel secondo insieme: le classi senza la ventilazione meccanica.

Questa comparazione era strutturata analizzando i dati dell’incidenza (i nuovi casi positivi) da Sars-CoV-2 nei due insiemi oggetto di osservazione, classi con VMC vs classi senza ventilazione. Questo studio è stato strutturato attraverso il coinvolgimento di tutti gli ordini di scuola, dalla scuola dell’infanzia alla scuola secondaria superiore.

Su questa premessa la Fondazione Hume ha chiesto alla Regione Marche di poter analizzare i dati raccolti, in modo da stimare l’efficacia della VMC nel contrastare la trasmissione dell’infezione.

A questo scopo sono stati costruiti un certo numero di modelli matematico-statistici, atti a valutare l’impatto della VMC sul rischio di trasmissione, al netto di altri effetti quali l’ordine della scuola e il numero di alunni per classe.

2. Metodi

Per stimare l’efficacia della Vmc sono stati usati 2 indicatori di trasmissione, basati sul conteggio dei cluster di casi (2 o più casi entro la medesima classe). L’impatto della Vmc è stato valutato sia in modo grezzo, ovvero confrontando i valori dei due indicatori su fasce di classi omogenee quanto al numero di ricambi-ora, sia con tecniche di regressione, tenendo sotto controllo il numero di alunni per classe e il tipo di scuola.

Fra le molte stime di efficacia della Vmc ottenute, di norma sono state selezionate le più prudenti.

3. Risultato principale

Il rischio di trasmissione si può stimare calcolando, per ogni classe, il rapporto fra numero di casi attribuibile ad infezioni avvenute entro la classe e il numero di esposti, ossia di alunni per classe.

Ponendo a 100 il valore dell’indicatore per le classi prive di VMC si può determinare il rischio relativo di infezione per le aule dotate di VMC. Tale rapporto è pari al 37.2%, il che vuol dire che la presenza della VMC in classe abbatte il rischio di trasmissione di un fattore vicino a 3 (indicatore medio).

La portata massima degli apparecchi installati varia notevolmente da scuola a scuola, in un range che va da 100 a 1000 metri cubi-ora. Se distinguiamo le classi in base alla portata degli apparecchi installati, scopriamo che il rischio relativo può scendere intorno a un valore compreso fra 5 e 6 se la portata supera i 750 metri-cubi ora, il che equivale – approssimativamente – a 5 ricambi-ora.

Si può riassumere tutto questo calcolando come cresce il fattore di abbattimento del rischio man mano che sale la qualità della VMC, misurata dal numero di ricambi-ora.

Come indicato nella tabella 1.2 l’indicatore di trasmissione varia in base alla presenza di scuole con VMC/senza VMC o con una differente portata di metri cubi/ora della VMC. Si osserva una variazione dell’efficacia da: 40% correlata ad un ricambio/ora di 0,67-3,33, ad un 66,8% di efficacia correlata a 3,33 – 4,67 ricambio/ora a 82,5% di efficacia con 4,67-6,66 ricambio/ora.

Si vede bene che la VMC, specie se adeguatamente dimensionata (6 o più ricambi-ora), ha una capacità di abbattere il rischio di infezione da Sars-CoV-2 di oltre l’80%. Utilizzandola nelle scuole, si potrebbe passare da un tasso di Incidenza di 250 su 100.000 (soglia di rischio individuata dal Ministero) a un tasso di 50 su 100.000 con l’abbattimento di massimo di efficacia.

Sorprendentemente, il fattore di abbattimento del rischio (compreso fra 5 e 6), desunto da questa ricerca sul campo, corrisponde perfettamente a quello ricavabile dagli studi degli ingegneri ed esperti di qualità dell’aria, basati su esperimenti controllati (vedi

Mikszewski, A., Stabile, L., Buonanno, G., Morawska, L., Increased close proximity airborne transmission of the SARS-CoV-2 Delta variant, Science of the Total Environment, 816, 2022).

4. Notizie sui dati

Il data set finale è costituito da un file con 10465 record (pari al numero delle classi), ciascuno descritto da 21 variabili (più i campi identificativi della classe e della scuola).

Le variabili fondamentali che descrivono ogni classe sono le seguenti:

• provincia
• plesso
• ordine della scuola
• sezione
• annualità
• numero di alunni della classe
• numero di studenti positivi in 12 periodi diversi
• presenza/assenza della VMC
• marca impianto VMC
• modello impianto VMC

I 12 periodi considerati corrispondono alle settimane, salvo il periodo iniziale, che va dal 13 settembre al 10 ottobre, e il periodo finale, che va dal 7 al 31 gennaio.

Le classi considerate sono tutte quelle senza Vmc (10125), più tutte quelle dotate di Vmc fin dal 13 settembre (316 su 340): in tutto 10441 classi.

Infine, ecco alcune informazioni sintetiche sulle classi considerate.

Per questa prima fase di studio, la percentuale di classi presa in esame è pari al 3% del totale.

L’analisi completa sarà disponibile nei prossimi giorni

Ci risiamo. Come lo scorso anno alle politiche, come nelle precedenti amministrative, come (quasi) sempre in tutti i tipi di consultazione elettorale dell’ultimo decennio almeno, conoscere in anticipo le tendenze del voto degli italiani è una chimera.

La serata del 26 maggio scorso è parsa a tutti una riedizione dell’incubo dell’anno precedente. Exit-polls che non avevano nulla a che vedere con i risultati reali, come avremmo scoperto qualche ora dopo, solamente grazie ai costanti – ma comunque sempre lenti – aggiornamenti del sito Eligendo, del Viminale. Prime proiezioni che si allontanavano, poco alla volta, dai precedenti exit-polls, ma con stime che restavano ancora molto distanti, pur con qualche meritoria eccezione, dalle percentuali di voto che avremmo saputo solo alle prime ore del mattino seguente.

Passi per le televisioni private, Sky o La7, ma se il servizio pubblico della Rai, con i soldi dei contribuenti, mette in scena uno spettacolo politico-giornalistico basato sulle stime di voto, e queste stime sono del tutto erronee, ci troviamo a chiederci: perché dobbiamo buttare i nostri soldi in questo modo? Perchè non seguire invece l’evoluzione dello scrutinio reale dei voti fornitoci del Ministero degli Interni che, oltretutto, è molto più divertente.

Tanto da assomigliare quasi ad un campionato di calcio: dopo le prime giornate è in testa il Partito Democratico, tallonato dal Movimento 5 stelle; ma ecco che nel girone di ritorno torna a farsi avanti la Lega di Salvini, che domina le ultime 10 partite e arriva trionfante ad aggiudicarsi la prima piazza, con un distacco piuttosto sensibile sugli altri contendenti. Scudetto aggiudicato, mentre sono relegate in serie B +Europa e La sinistra, capitanate da Bonino e Fratoianni, che non raggiungono il quorum necessario per restare nella massima serie. Un divertimento puro, anziché la rabbia di non capire se stiamo assistendo a reali anticipazioni di ciò che poi accadrà davvero, oppure a semplici numeri casuali, con beneficio di inventario.

Ora, sappiamo ormai molto bene che le stime prodotte dai sondaggi sono abbastanza deboli, abbastanza aleatorie, sempre più difficilmente veritiere. L’ho scritto qualche settimana fa proprio su questo sito: dieci buone ragioni per cui non credere (troppo) ai sondaggi. In particolare quelli sulle stime sul voto, perché questo è sempre più volatile, meno ancorato all’appartenenza socio-politica (la fedeltà pesante), meno determinato dalla vicinanza ideologica tipico della fedeltà leggera (berlusconiani contro anti-berlusconiani) e sempre più pragmatico ed emozionale. Il tradimento non genera più sensi di colpa, nella vita come nelle urne. Si può fare tutto, come già profetizzava Giorgio Gaber 40 anni fa.

I sondaggi dovrebbero essere in grado di capire dunque, più dell’elettore, quello che lui ancora non sa, cioè per quale partito voterà, anticipando le sue scelte finali: un compito quasi impossibile. Ma se gli errori nei sondaggi sono comprensibili, entro certi limitati, quelli negli exit-polls certamente un po’ meno, soprattutto perché la scelta finale l’elettore l’ha appena fatta, e dunque l’incertezza precedente è stata già risolta. Qui i problemi da superare sono di tre tipi: la desiderabilità sociale, il numero di sedi-campione esiguo e il sistema di rilevazione.

La desiderabilità sociale, vale a dire la scarsa volontà di dichiarare un partito non troppo ben visto dall’opinione pubblica, antica distorsione dei tempi della Democrazia Cristiana o del Berlusconi in crisi, pare essere ormai superata quasi del tutto. Sdoganata ogni possibile scelta politica, non ci si “vergogna” più di nulla, nemmeno del voto per Casa Pound, in sospetto neo-fascismo. E dunque, trovarsi con exit-polls dove la Lega veniva data da tutti con una forchetta tra il 27 ed il 30 per cento, come hanno fatto praticamente tutti gli Istituti di ricerca, sotto-stimandola di una quota compresa tra i 4 e i 7 punti, è un deciso errore che andrebbe sanzionato. Così come le stime del M5s, sovra-stimato in egual misura.

Le cause potrebbero essere individuate nella scarsa numerosità dei punti di campionamento. Se intervisto gli elettori di sole 30-40 sedi di voto, è possibile che i miei risultati saranno ampiamente distorti. Meglio non effettuare nulla in quel caso. E se così si fa perché i committenti non danno abbastanza soldi, ancor meglio astenersi, indicando loro il numero minimo di interviste da effettuare all’uscita dei seggi, altrimenti si declina l’incarico. Ma così non si fa. Si prendono i graditi compensi, sbagliando nettamente le previsioni, tanto chi ci rimette è il cittadino; il ricordo dell’errore sfumerà qualche ora dopo, quando i risultati reali verranno diffusi dal Viminale.

Ultimo possibile errore, il sistema di rilevazione o il modello di stima che non funziona. E in questo caso, inutile sottolinearlo, quegli Istituti dovrebbero chiudere definitivamente i battenti, almeno in questo campo, dopo almeno 30 anni di exit-poll, in Italia e nel mondo.

Infine, le proiezioni. In questo caso, l’errore è quasi “impossibile”, se si hanno a disposizione un numero di sezioni-campione minimamente affidabile, poiché si tratta unicamente di rilevare, attraverso appunto questo campione di sezioni, ciò che è accaduto nella popolazione elettorale nel suo complesso. E a chiusura dei seggi, domenica 26 maggio, ci siamo trovati sul video tre stime del tutto differenti: la Lega, il cui risultato finale è stato come noto del 34,3%, veniva data al 27%, al 29% e al 31%, nelle prime proiezioni. Errori di stima tra il 7,3% e il 3,3%: inammissibile.

Gli Istituti di ricerca che si esibiscono in queste performance dovrebbero venir valutati sulla base della loro efficienza. Se si sbagliano in maniera a volte clamorosa le stime degli exit-polls e, soprattutto, quelle delle proiezioni, si dovrebbe essere squalificati, come con il cartellino rosso nel calcio, almeno per un turno. Ma questo non accade.

Perché? Molto semplice. Si vincono le gare grazie al ribasso dei costi, e questo inevitabilmente porta ad un abbassamento della numerosità campionaria e ad una minor capacità previsiva dei campioni utilizzati, troppo ridotti. Gli errori devono (e possono) venir contenuti, fin dalla prima proiezione, ad un massimo dell’1-1,5%, e non possono essere superiori allo 0,5-0,8% all’ultima proiezione. Ma da anni questa efficienza non si raggiunge più. E non si incorre in nessuna “sanzione”, se non quella economica, forse.

E’ una sorta di “spirale dell’inefficienza”: i committenti (e se sono pubblici è altamente riprovevole) spendono meno e danno un servizio pessimo, con un risparmio ulteriore se tagliano i compensi in caso di errore; gli Istituti risparmiano sui propri costi, fornendo un servizio inutile, ma rientrano delle proprie spese, con un parallelo investimento pubblicitario sostanzialmente gratuito. E così continuerà, se qualcuno non fermerà la macchina.

Da anni, da quando ho iniziato ad occuparmi di sondaggi, soprattutto politici ma non solo, ho sempre fatto riferimento ad uno strano decalogo, quasi un decalogo all’incontrario: 10 buoni motivi per cui è opportuno non credere ai sondaggi, o meglio, ai risultati di un sondaggio. Gli errori insiti nel procedimento demoscopico sono così numerosi che, anche a cercare di far le cose in maniera il più corretta possibile, è quasi impossibile arrivare ad una soluzione che rispecchi esattamente il pensiero della popolazione di riferimento. Ci si può avvicinare, certo, ma con grandi margini di imprecisione.

Pensate soltanto ai quotidiani sondaggi sulle intenzioni di voto. Si utilizzano campioni di un migliaio di casi, quando va bene, per stimare partiti che a volte stanno attorno al 4%, e che con il classico “errore di campionamento” del 2-3% potrebbero valere dall’1% al 7%. Senza senso. Ma anche per le forze politiche più robuste le stime rimangono parecchio aleatorie. Su 1000 persone che rispondono, almeno 350-400 sono indecisi o astensionisti, e già qui il campione si riduce a 600 casi, con un margine di errore che sale a +/- 4%. Quindi, se ottengo una percentuale di consensi per la Lega, ad esempio, pari al 32%, vorrà dire che sono quasi certo che la Lega viaggia tra il 28% ed il 36%. Tutto e il contrario di tutto: se fosse al 28%, sarebbe in crisi, al 34% sarebbe in gran spolvero. Sostanzialmente, quel sondaggio non mi serve a niente, non mi dice nulla di più di quanto non sapessi già.

E questo per limitarci al solo errore statistico “misurabile”. Mentre nulla sappiamo di tutte le altre distorsioni non quantificabili: le sostituzioni del campione, l’auto-selezione dei rispondenti, l’errore di rilevazione, le bugie consapevoli e inconsapevoli, gli “auto-inganni”, l’influenza del mezzo di rilevazione, la desiderabilità sociale, la ristrutturazione del ricordo di voto, le risposte acquiescenti, l’impatto dell’intervistatore, l’aleatorietà delle opinioni e così via.

Last ma non certo least, il cosiddetto “wording”, vale a dire la scelta delle parole utilizzate per porre una certa domanda, che ha una influenza a volte così decisiva sui risultati dei sondaggi che in alcune occasioni le opinioni di campioni della popolazione, interrogati nello stesso giorno da due istituti di ricerca differenti, divergevano nettamente le une dalle altre.

Il caso più noto ci riporta a quanto avveniva negli USA durante la guerra del Vietnam: i quotidiani pro-intervento pubblicavano sondaggi in cui emergeva come la maggioranza degli americani fosse favorevole a “proteggere il popolo vietnamita (e americano) dall’influenza sovietica”; i quotidiani anti-interventisti pubblicavano viceversa sondaggi dove la maggioranza si dichiarava contraria a “mandare i propri figli a combattere e a morire in Vietnam”. Ma tutti i giornali titolavano semplicemente: “Gli americani sono a favore (oppure contro) il ritiro delle truppe”.

Questo esempio, unitamente a molti altri dello stesso tenore, ci induce infine a porci la cruciale domanda: fino a che punto è possibile “manipolare” un sondaggio, indirizzare cioè già dalla formulazione delle domande gli esiti delle interviste, ancora da realizzare? Per tentare di rispondere a questo quesito ho condotto un esperimento, in un mio recente laboratorio universitario. Ho redatto due questionari sulla qualità della vita a Milano, uno mirato ad ottenere un esito “positivo” e l’altro “negativo” su numerosi aspetti della vita milanese, e in particolare sulla accoglienza del programmato incremento di 50 centesimi del biglietto dei trasporti pubblici, deciso dal Comune.

Ho mandato poi gli studenti del laboratorio ad effettuare 600 interviste a due campioni gemelli con i due diversi questionari. I risultati hanno certificato, almeno in parte, le aspettative. I giudizi sugli aspetti considerati differiscono di quasi 20 punti percentuali tra il “positivo” e il “negativo”, con differenze piuttosto significative (oltre il 30%) per quanto riguarda soprattutto la dotazione commerciale, la manutenzione stradale e, come c’era da aspettarsi, il tema dell’immigrazione e dell’integrazione. Meno evidente, inaspettatamente, il “distacco” sul problema della sicurezza percepita.

In generale, peraltro, la buona percezione della qualità della vita a Milano è stata ribadita in entrambi gli approcci, con un livello di soddisfazione comunque elevato, costantemente superiore al 70% di giudizi positivi. Segno evidente che, se la gente è abbastanza soddisfatta, risulta difficile indurla alla negatività, anche con strumenti manipolatori.

C’è però un dato, infine, che getta una luce obliqua sulle capacità manipolatorie del “wording”, ed è quello che riguarda il giudizio sull’incremento del biglietto dei mezzi di trasporto. In questo caso, le differenze sono davvero molto sensibili: con l’approccio “positivo” l’opinione favorevole all’aumento del costo è pari al 69%, con quello “negativo” si riduce ad un misero 22%. Un abisso.

Che cosa farà dunque un’Amministrazione comunale “perversa” per far accettare ai suoi cittadini una qualsiasi propria iniziativa? Semplicemente, diffonderà con molta enfasi risultati di sondaggi manipolati, in cui risulta che la popolazione è particolarmente favorevole a quella iniziativa. Attenzione, dunque, quando appaiono sui giornali titoli evocativi di sondaggi effettuati: è opportuno, in ogni occasione, non fidarsi. Meglio andare a verificare “come” sono state poste le domande.

Nel 2008 Leo Knüsel ha introdotto un nuovo metodo con cui affrontare il problema della rotazione nell’analisi fattoriale, problema che consiste nel trovare una matrice di rotazione T da applicare ad una matrice iniziale di loading (A) al fine di produrre una matrice di loading ruotata (L= AT) in cui le relazioni tra variabili manifeste e fattori latenti siano più nitide e rendano così più agevole l’interpretazione dei fattori latenti. Con il metodo Chisquaremax, la matrice dei quadrati dei loading viene considerata alla stregua di una tabella di contingenza e la matrice di rotazione T viene scelta in modo da rendere massima l’associazione tra le righe (variabili manifeste) e le colonne (fattori latenti). Il metodo può essere applicato a rotazioni sia ortogonali sia oblique, qui viene considerato soltanto il caso di rotazioni ortogonali.

Chisquaremax possiede due caratteristiche in particolare che lo rendono una interessante alternativa ai numerosi criteri disponibili in letteratura:

• tratta in modo simmetrico le righe e le colonne, a differenza di altri metodi che tendono a semplificare unicamente il profilo delle righe (metodo Quartimax) o ad assegnare comunque un peso maggiore alla semplicità delle righe rispetto a quella delle colonne (come in generale i metodi della famiglia Orthomax);
• non tende a produrre un fattore generale, cioè una colonna su cui saturano molte variabili manifeste, aspetto che caratterizza il metodo Quartimax e neppure a produrre colonne di loadings con la stessa somma dei quadrati, aspetto che caratterizza il metodo Varimax.

La versione dell’algoritmo resa disponibile dall’autore nel lavoro del 2008, tuttavia, non prevede la possibilità di operare la normalizzazione di Kaiser e prevede che la matrice di rotazione iniziale sia unicamente una matrice identità. In questo contributo viene proposta una versione “arricchita”, più generale, che consente:

1. di applicare la normalizzazione di Kaiser
2. di usare una matrice di rotazione iniziale random o di ottenere la miglior soluzione all’interno di un certo numero di soluzioni prodotte variando la matrice random di rotazione iniziale.

In appendice viene riportato un esempio di applicazione della funzione “arricchita”, gen.chi2max, e lo script in R.

Riferimenti bibliografici

Harman, H. H. (1976). Modern factor analysis. University of Chicago Press.

Knüsel, L. (2008a). Factor analysis: Chisquare as rotation criterion. Technical Report Number 040, Department of Statistics, University of Munich.

Knüsel, L. (2008b). Chisquare as a rotation criterion in factor analysis. Computational Statistics & Data Analysis, 52(9), 4243-4252.

APPENDICE

Esempio di applicazione
La matrice non ruotata A è tratta da Harman (1967, p.186).
Le soluzioni con e senza normalizzazione di Kaiser sono state prodotte con:
gen.chi2max(Mat, b=1000, c=1e-09, d=0, e=50, s=127, g=1)
gen.chi2max(Mat, b=1000, c=1e-09, d=1, e=50, s=127, g=1)

in cui:

Mat = la matrice A, non ruotata
b = numero di iterazioni
c = criterio di convergenza
d = normalizzazione di Kaiser (1=attiva; 0= non attiva)
e = numero di matrici random di rotazione iniziale (e= -1 una sola matrice random; 0= matrice identità; >0 più di una matrice random iniziale)
s = seme per la generazione delle matrici random
g = parametro gamma (vedi Knüsel, 2008a)

Come si osserva dalla tabella, il valore della funzione obiettivo (FOB) cresce passando dalla matrice non ruotata a quelle ruotate, inoltre la soluzione con normalizzazione di Kaiser è leggermente migliore rispetto a quella ottenuta senza la normalizzazione.

Con altre matrici tratte da esempi reali o generate casualmente l’applicazione della normalizzazione di Kaiser non sempre produce un miglioramento della FOB (talvolta produce i medesimi risultati, altre volte un peggioramento della FOB), anche l’utilità di ricorrere a più matrici random di rotazione iniziale dipende dalla matrice di loading inziale.

Script in R

N.B.
La funzione di massimizzazione del Chi quadrato è tratta da Knüsel (2008b).
E’ richiesto il package di R: GPArotation

chi2max.0 = function(x,TT,gamma, bb,cc,dd)
{
x=as.matrix(x)
nc=ncol(x)
 if(missing(bb)) bb=1000
 if(missing(cc)) cc=1e-9
 if(missing(dd)) dd=0
 if(missing(TT)) TT=diag(nc)
 if(missing(gamma)) gamma=1
eps=cc
if (nc<2)
 return(x)
p=nrow(x)
k=ncol(x)
c=0
d=0
z=x%*% TT
 if (dd==0){
H=drop(z^2%*%rep(1,k)) 
 # ss rows (comunalità)
 for (i in 1:bb) {
 D=drop(rep(1,p)%*% z^2 )
 E=drop((1/H) %*% z^4)
 C=diag(1/H) %*% z^3 %*% diag(1/D) - (1/2) * z %*% diag(E) %*% diag(1/D^2)
 B=t(x) %*% C
 sB=La.svd(B)
 TT= sB$u %*% sB$vt
 dpast=d
 d=sum(sB$d)
 zpast=z
 z=x%*% TT
 D=drop(rep(1,p) %*% z^2 ) 
 cpast=c
 c=sum( diag(1/H) %*% z^4 %*% diag(1/D) )
 if (abs(d-dpast)/d < eps && abs(c-cpast) /c < eps && abs(d-c/2)/d < eps)
 break
 z=gamma*z + (1-gamma)*zpast 
 }
 }
 if (dd==1){
 uM=t(rep(1,p))
 uH=rep(1,k)
 # comunalità
 c.st=(x^2%*%uH)
 C.st=c.st%*%uH
 xk=x/(C.st^0.5)
 z=xk%*% TT
 H=drop(z^2%*%rep(1,k)) 
 for (i in 1:bb) {
 D=drop(rep(1,p)%*% z^2 )
 E=drop((1/H) %*% z^4)
 C=diag(1/H) %*% z^3 %*% diag(1/D) - (1/2) * z %*% diag(E) %*% diag(1/D^2)
 B=t(xk) %*% C
 sB=La.svd(B)
 TT= sB$u %*% sB$vt
 dpast=d
 d=sum(sB$d)
 zpast=z
 z=xk%*% TT
 D=drop(rep(1,p) %*% z^2 ) 
 cpast=c
 c=sum( diag(1/H) %*% z^4 %*% diag(1/D) )
 if (abs(d-dpast)/d < eps && abs(c-cpast) /c < eps && abs(d-c/2)/d < eps)
 break
 z=gamma*z + (1-gamma)*zpast 
 }
 z=z*(C.st^0.5) 
 }
list(iterations = i,Table=matrix(c(c,d),1,2), Th=TT, loadings=z, SS_columns=rep(1,p)%*%z^2)
}
gen.chi2max=function(X,b,c,d,e,s,g) {
X=as.matrix(X)
if(missing(b)) b=1000
if(missing(c)) c=1e-9
if(missing(d)) d=0
if(missing(e)) e=50
if(missing(s)) s=127
if(missing(g)) g=1
kais=list(FALSE,TRUE)
dd=d+1
P=nrow(X)
M=ncol(X)
M.it=diag(ncol(X))
if (e==-1){
set.seed(s)
M.it=Random.Start(M)
}
out0=chi2max.0(X,TT= M.it, gamma=g, bb=b,cc=c,dd=d)
 Qr=out0$Table[nrow(out0$Table),1]
 Mr=M.it
 Zr=out0$loadings
 Tr=out0$Th
if (e>0){
 set.seed(s)
 n.rand=e
 for (ii in 1:n.rand){
 M.it=Random.Start(M)
 out=chi2max.0(X,TT= M.it, gamma=g, bb=b,cc=c,dd=d)
 Qpast=Qr
 Mpast=Mr
 Zpast=Zr
 Tpast=Tr
 Qr=out$Table[nrow(out$Table),1]
 Mr=M.it
 Zr=out$loadings
 Tr=out$Th
 if (Qr<Qpast) {
 Qr=Qpast
 Mr=Mpast
 Zr=Zpast
 Tr=Tpast
 }
 }
}
list(fob=Qr, rotmat=Tr, loadings=Zr,SS_columns=rep(1,P)%*%Zr^2)
}